我有上本週4/19的課
7.題目
設有三桿相連結成端桿(dyad)之型式。請利用網路講義中之函數dyad及dyad_draw作分析。
function dyad_draw(rho,theta,td,tdd)
其中:
* 各桿之對應長度rho=[a, a+5, a-5]cm,a=(你的學號末一碼)+10;
* 各桿之對應起始角度theta=[0, 0, 0]度;
* 各桿之對應角速度為td=[0.2, 0.5, 0 .3]rad/s;
* 各桿之對應角加速度為tdd=[0, 0.1, 0.2]rad/s^2;
問:
1. 當t=[1 2 3 4 5]秒時,此端桿之對應方位如何?
2. 繪出三桿之結點之速度,加速度與時間t之關係。
3. 能作出此時間區段之動畫嗎?
Ans:
(1)
首先,按題目所示,引用網路講義裡的兩個函式如下:
*******************************************************************
function [vec, dyadata] = dyad(rho,theta,td,tdd)
%
% function [vec, th, dyadata] = dyad(rho,theta,td,tdd)
% Analyzes a dyad linkage composing a crank and a dyad.
% Inputs: rho:length of links
% theta:incling angles, deg.
% td:angular velocity, rad/s
% tdd:angular acceleration, rad/s^2
% Outputs: vec:absoute length of links
% th:angles of links, velocities & acc, deg
% dyadata:original data, in complex forms
% Example:[vec,th,dyadata] = dyad([5 10],[30 50],[2 4])
theta=theta(:); rho=rho(:);
n=length(rho);
if nargin<4, tdd="zeros(size(rho));" nargin="=" td="ones(size(rho));" td="ones(size(rho))*td;end" tdd="ones(size(rho))*tdd;end" td="td(:);tdd=" d2g="pi/180;" tt="exp(i*theta*d2g);" pp="rho.*tt;" vv="i*td.*pp;" aa="-pp.*td.^2+i*pp.*tdd;" dyadata="[pp" vec="[abs(sum(dyadata));angle(sum(dyadata))/d2g];" x="[0;cumsum(real(data(:,1)))];y=" i="1:length(x)-1" k="1:length(rho)" x0="x(k+1);y0=" vx="x0+real(data(k,2));vy=" ax="x0+real(data(k,3));ay=" sdata="sum(data);" ss="[real(sdata(1))" vv="[real(sdata(2))" aa="[real(sdata(3))" nargin="=" dd="1;end;" d="abs(dd);" ab="(B(1)+j*B(2))-(A(1)+j*A(2));" d="abs(AB);th=" t="linspace(pi/2,2.5*pi,20);" cout="max(d/2,0.2)*exp(j*t');Cin=">0,
P=[0;Cin;Cout(1:10);D+Cout(11:20);D+Cin;D+Cout(20);Cout(1)];
else
P=[Cin;0;D;D+Cin];
end
xx=real(P);yy=imag(P);
x=xx*cos(th)-yy*sin(th)+A(1);
y=xx*sin(th)+yy*cos(th)+A(2);
line(x,y)
axis equal
************************************************************************
(註:個人決定再引用網路講義中另一個函數linkshape,這可使圖形美觀.)
dyad_draw([12,17,7],[0,0,0],[0.2,0.5,0.3],[0,0.1,0.2]);
for n=0:1:5;
dyad_draw ([12,17,7],[0.2*n,0.5*n+(1/2)*0.1*n^2,0.2*n+(1/2)*0.2*n^2],[0.2,0.5+n*0.1,0.3+0.2*n],[0,0.1,0.2]);
pause(1);
end;
%在此,我使用了一些數學運算代入dyad_draw這個function裡面.
%由於角速度以及角加速度隨時間而變,所以設一n變數進去,使其模仿時間.
%利用for迴圈,使他重複執行五遍,便可得下列圖片之結果.
當t=[1 2 3 4 5]秒時,此端桿之對應方位:
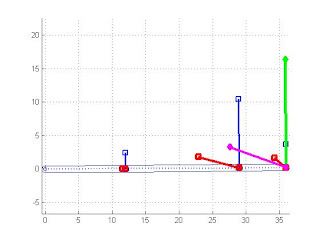
第1秒

第2秒
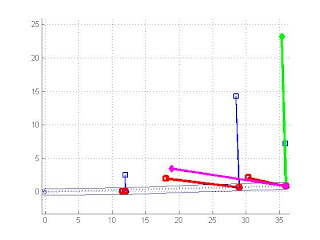
第3秒

第4秒

第5秒
(2)
第一桿之速度
第一桿之加速度


第二桿之速度
第二桿之加速度
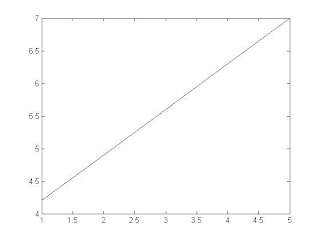

第三桿之速度
第三桿之加速度
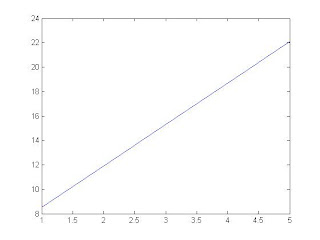
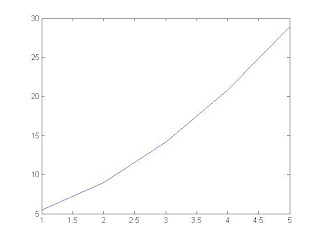
%以上繪圖來自於dyad_draw,利用其角速度以及角加速度的值去跑出來的.
%簡單來說,就是利用第一題的程式,把其得到的值代入另一個繪圖小程式.
%這個程式是用plot畫出來的,順著桿長最大極限而畫出的.
%類似這個:
for a=1:length(rho)
figure
plot(aa(j,:))
figure
plot(bb(j,:))
end
%當初禮拜六畫這個圖的時候,代數好像不是用這個(忘了),不過概念上大概長這個模樣就是了.
(3)
axis equal;
dyad_draw([12,17,7],[0,0,0],[0.2,0.5,0.3],[0,0.1,0.2]);
pause(2)
clf
for n=1:5
axis equal;
dyad_draw([12,17,7],[0.2*t,0.5*t+0.5*0.1*t^2,0.3*t+0.5*0.2*t^2],[0.2,0.5+t*0.1,0.3+t*0.2],[0,0.1,0.2]);
pause(1)
clf
end;
%與第一題的作法雷同,加了些暫停,使其運作更流暢.
hw7動畫





